GSVA
Gene Set Variation Analysis is a method to calculate genesets pathway scores across different samples.
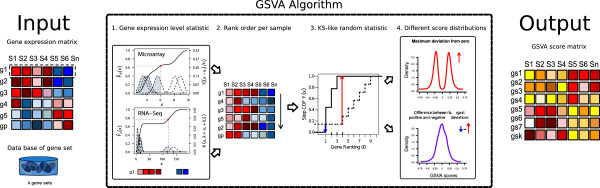
Firstly, there has an input gene expression matrix. We perform non-parametric kernel estimation of a specific gene's cumulative density function.
In the case of microarray data, a Gaussian kernel is used:
\(\widehat{F}_{h_i}\left(x_{i j}\right)=\frac{1}{n} \sum_{k=1}^n \int_{-\infty}^{\frac{x_{i j}-x_{i k}}{h_i}} \frac{1}{\sqrt{2 \Pi}} e^{-\frac{t^2}{2}} d t\)
In the case of RNA-seq data, a discrete Poisson kernel is employed:
\(\widehat{F}_r\left(x_{i j}\right)=\frac{1}{n} \sum_{k=1}^n \sum_{y=0}^{x_{i j}} \frac{e^{-\left(x_{i k}+r\right)}\left(x_{i k}+r\right)^y}{y !}\),
The cumulative density function is estimated for every gene using all samples from the above distributions. In simpler terms, a CDF value is assigned to each gene in each sample.
With the CDF of all genes in each sample, we sort them from largest to smallest.
Secondly, we normalize the rank values. \(r_i\) is the rank value of the gene \(i\) in sample \(S\), \(p\) is the gene number.
\(z_{i j}=\left|\frac{p}{2}-r_i\right|\)
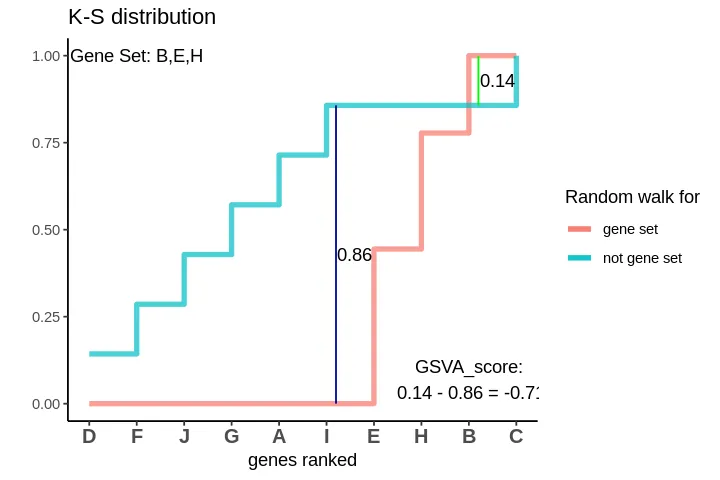
Thirdly, to calculate \(ES(s)\) with sort \(z_{i j}\)
\(\nu_{j k}(\ell)=\frac{\sum_{i=1}^{\ell}\left|r_{i j}\right|^\tau I\left(g_{(i)} \in \gamma_k\right)}{\sum_{i=1}^p\left|r_{i j}\right|^\tau I\left(g_{(i)} \in \gamma_k\right)}-\frac{\sum_{i=1}^{\ell} I\left(g_{(i)} \notin \gamma_k\right)}{p-\left|\gamma_k\right|}\),
\(E S_{j k}^{\text {diff }}=\left|E S_{j k}^{+}\right|-\left|E S_{j k}^{-}\right|=\max _{\ell=1, \ldots, p}\left(0, v_{j k}(\ell)\right)-\min _{\ell=1, \ldots, p}\left(0, v_{j k}(\ell)\right)\),